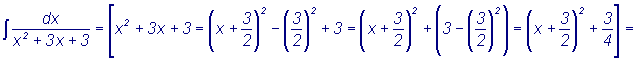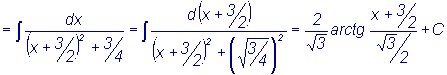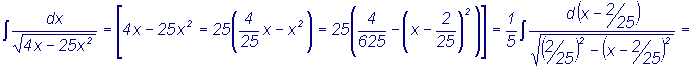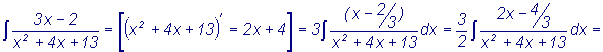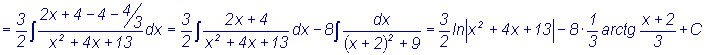| Темы | Предыдущий пункт | Следующая лекция | Литература | |
|
|
|
Лекция 4.2. 
Методы интегрирования |
|
|
|
|
|
4.2.3. Интегралы, содержащие квадратный трехчлен в знаменателе. |
|
|
К такому виду относятся интегралы: Интегрирование выражений I - го типа производится путем выделения полного квадрата в квадратном трехчлене и последующего применения формул табличных интегралов 8-11. Напомним, если в интеграле квадратный трехчлен имеет вид
ax2+bx+c, то для выделения полного квадрата a выносят
за скобки Примеры 1. 2. Выражения II-го типа разбиваются на сумму двух интегралов,
путем выделения в числителе производной от трехчлена, стоящего в
знаменателе.
Так как (ax2+bx+c)I = 2ax+b,
то d(2ax+b) = d(ax2+bx+c) и можно записать
Аналогично можно представить
Пример
|
|
; 
;
; 
.
и затем применяют
формулу для приведенного квадратного трехчлена 
I тип интеграла.
II тип интеграла.
|
|
|
|