Рассмотрим интегралы от некоторых иррациональных функций, которые с
помощью определенных подстановок приводятся к интегралам от рациональных
функций новой переменной.
1. Интегралы вида 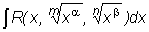 сводятся
к рациональной функции подстановкой x = tN, где N
- наименьшее общее кратное (НОК) m и n.
сводятся
к рациональной функции подстановкой x = tN, где N
- наименьшее общее кратное (НОК) m и n.

Пример
:
Найти 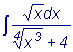 .
.
Так как НОК (2, 4) = 4, то соответствующая подстановка
x = t4
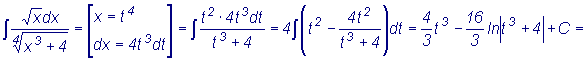
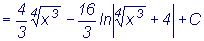
2. Интегралы вида 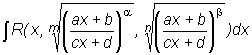 , где R
- рациональная функция, a, b, c, d - постоянные, приводится к
интегралу от рациональной функции нового аргумента с помощью подстановки
, где R
- рациональная функция, a, b, c, d - постоянные, приводится к
интегралу от рациональной функции нового аргумента с помощью подстановки
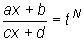 , где N - наименьшее
общее кратное m и n.
, где N - наименьшее
общее кратное m и n.

Пример
:
Найти 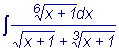 . НОК(2, 3, 6)=6.
. НОК(2, 3, 6)=6.
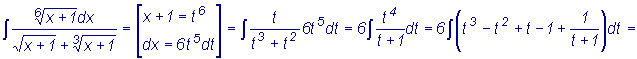
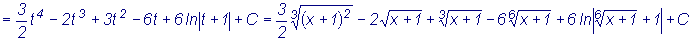
3. Иррациональные функции вида 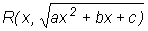 выделением полного квадрата сводятся к 3-м видам функций, для каждой из
которой применяется свой вид подстановки:
выделением полного квадрата сводятся к 3-м видам функций, для каждой из
которой применяется свой вид подстановки:
1). 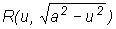 ,
подстановка
,
подстановка 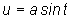 ;
;
2). 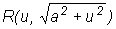 ,
подстановка
,
подстановка 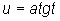 ;
;
3). 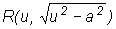 ,
подстановка
,
подстановка 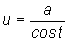 .
.

Примеры
:
1. 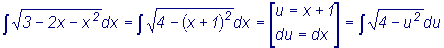
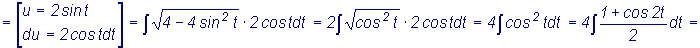
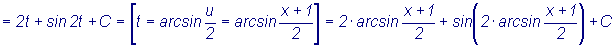
.2. 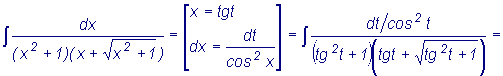
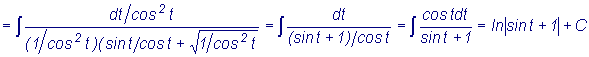
Для того чтобы перейти от новой переменной
t к переменной x,
воспользуемся формулами тригонометрии. Так как 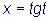 ,
то
,
то 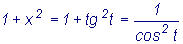 . Поэтому
. Поэтому
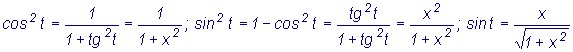
Окончательный ответ: 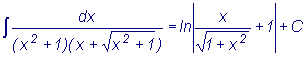 .
.
 Задачи
для самостоятельного решения.
Задачи
для самостоятельного решения.

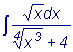 .
. 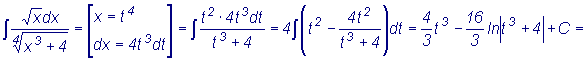
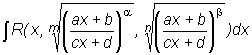 , где R
- рациональная функция, a, b, c, d - постоянные, приводится к
интегралу от рациональной функции нового аргумента с помощью подстановки
, где R
- рациональная функция, a, b, c, d - постоянные, приводится к
интегралу от рациональной функции нового аргумента с помощью подстановки
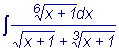 . НОК(2, 3, 6)=6.
. НОК(2, 3, 6)=6. 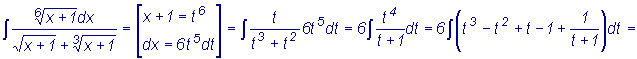
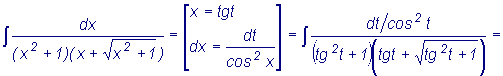
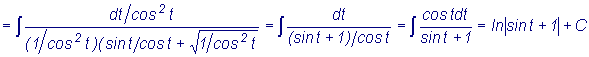
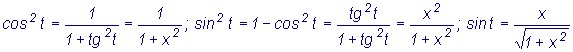
 .
.