ODE Lecture 6.1.

Лекция 1.2.

Векторная алгебра

1.2.1 Векторы, основные понятия и определения.

При изучении различных разделов физики, механики и технических дисциплин встречаются величины: которые в выбранной системе единиц вполне характеризуются заданием их численных значений. Такие величины называются скалярными (числовыми) . Например, длина, площадь, объем, масса, температура являются скалярными величинами. Существуют и такие величины, для определения которых задания лишь численных значений недостаточно, необходимо знать также их направление в пространстве. Такие величины называются векторными. Например, сила, перемещение материальной точки, направленность магнитного поля являются векторными величинами. Понятие вектора стало одним из понятий современной математики благодаря широкому использованию этого понятия в различных областях математики, механики, а также в технике.

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, теория поля, тензорный анализ, общая теория многомерного векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности.

В математике на векторной основе излагаются аналитическая и дифференциальная геометрии.

Известно, что существует несколько подходов к введению понятия вектора. На наш взгляд наиболее естественно ввести понятие геометрического вектора как направленного отрезка, чтобы эффективнее принять это понятие при изложении теории и решении задач.

Рис. 2.1.

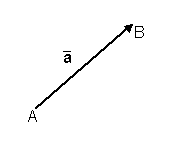
Определение 1.

Вектором называется направленный отрезок. Вектор обозначается либо символом (A - точка начала, В - точка конца), либо , на чертеже изображается стрелкой.

Определение 2. Длиной или модулем вектора называется длина отрезка АВ. Модуль вектора обозначается как .

В математике обычно рассматриваются свободные векторы, т.е. векторы, точка приложения которых может быть выбрана произвольно.

Определение 3. Вектор называется нулевым, если его начало и конец совпадают.

Рис. 2.2.

Нулевой вектор не имеет определенного направления и имеет длину, равную нулю. Любое направление можно считать направлением нулевого вектора. Геометрически нулевой вектор - это точка.

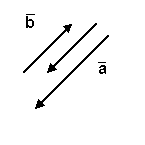
Определение 4. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарность векторов обозначают так : (рис. 2.2.).

Определение 5. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.

Определение 6. Вектор называется противоположными вектору , если модули их равны, а направления противоположны.

Рис. 2.3.

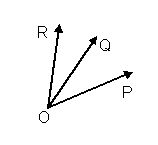
Определение 7. Векторы называются компланарными, если если они лежат в одной плоскости, или в параллельных плоскостях.

Определение 8. Пусть О - фиксированная точка. Тогда радиусом-вектором точки Р (относительно точки О) называют вектор . , , - радиусы-векторы (относительно точки О) (рис.2.3.).

Каждую точку пространства (плоскости) можно задавать радиусом-вектором.