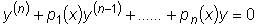| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Дифференциальные уравнения высших порядков |
|
|
|
|
|
6.2.3. Линейные уравнения высших порядков |
|
|
Дифференциальное уравнение n -го порядка называется
линейным, если оно линейно относительно неизвестной функции
y и ее производных
Линейное уравнение n -го порядка имеет вид:
Будем считать, что функции
Задача отыскания решения линейного дифференциального уравнения удовлетворяющего n начальным условиям: y(xo ) = yo , y I (xo ) = y Io ,.., y (n-1) (xo ) = y (n-1)o, при условиях непрерывности функций p1 (x), p2 (x) ,.., pn (x) , f(x), решается всегда, так как выполняются условия теоремы Коши.
В следующем параграфе будут установлены некоторые основные свойства линейных однородных уравнений.
При этом будут использованы прежде всего уравнения второго порядка.
|
|
|
|
|
|
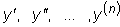 .
. 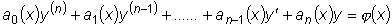 .
. 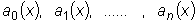 и
и
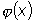 непрерывны, причем
непрерывны, причем
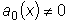 при всех значениях x
из той области, в которой мы рассматриваем уравнение.
при всех значениях x
из той области, в которой мы рассматриваем уравнение. 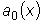 это уравнение может быть приведено к виду:
это уравнение может быть приведено к виду:
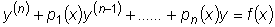 .
. 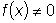 ,
то уравнение называется линейным неоднородным или уравнением
с правой частью.
,
то уравнение называется линейным неоднородным или уравнением
с правой частью.
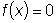 , то уравнение имеет
вид
, то уравнение имеет
вид