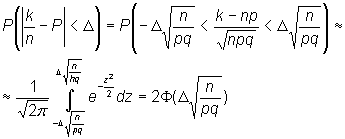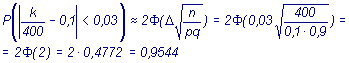Лекция 13.3

Повторение испытаний

13.3.2  Предельные теоремы в схеме Бернулли

Пример 1

Устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента в течение времени Т, равна 0,002. Найти вероятность того, что за время Т откажут ровно 3 элемента.

По условию задачи n = 1000, p = 0,002, k = 3, . Применим формулу Пуассона:

Пример 2 

Вероятность того, что станок - автомат производит годную деталь, равна .  За смену было изготовлено 280 деталей. Определить вероятность того, что среди них 20 бракованных. 

Решение. 

Согласно условию задачи имеем n = 280, k = 20, p = , q = . Находим:

По таблице значений функции находим . Искомая вероятность:

Локальная теорема Муавра – Лапласа позволяет оценить отдельные значения P_n(k) , то есть локальное поведение P_n (k) как функции k при больших n. Интегральная предельная теорема Лапласа позволяет оценить вероятность того, что событие А появится в n испытаниях от m₁ до m₂ раз.

Теорема 3. (Интегральная теорема Муавра - Лапласа)

Если вероятность p наступления события А в n независимых испытаниях постоянна и отлична от нуля и единицы, то при условии, что число испытаний достаточно велико, вероятность того, что в этих испытаниях событие А наступит от m₁ до m₂ раз, приближенно равна

где .

Ф(х) – функция Лапласа

Значения функции Лапласа Ф(х) берем из соответствующих таблиц, при этом Ф(-х) = - Ф(х).

Пример 3 

Вероятность того, что деталь не прошла проверку ОТК равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100.

Решение. 

Из условия задачи имеем p = 0.2, q = 0.8, n = 400, m₁ = 70, m₂ = 100. Тогда

По интегральной формуле Муавра – Лапласа имеем

Интегральная теорема Муавра – Лапласа позволяет оценить близость частоты и вероятности. Пусть р – вероятность успеха в схеме Бернулли и k – общее число успехов. Частотой успеха называется отношение .

Оценим вероятность события . Если n достаточно велико, то по формуле Лапласа имеем:

Пример 4

Вероятность того, что деталь не стандартна, р = 0,1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности по абсолютной величине не более, чем на 0,03. 

Решение. 

В качестве математической модели воспользуемся схемой Бернулли. По условию задачи имеем                             n = 400, p = 0,1, q = 0,9,

Часто возникает обратная задача: сколько нужно провести испытаний, чтобы частота отличалась от вероятности р не больше, чем на с вероятностью ( - мало)? Такого типа задачи возникают при использовании метода Монте – Карло (метод статистических испытаний). Идея метода заключается в моделировании случайного процесса или последовательных испытаний, вероятностные характеристики которых просто связаны с подлежащими вычислению величинами. В таких задачах естественно считать р неизвестным. Чтобы подобрать наименьшее n, при котором вероятность отклонения будет равна , нужно решить уравнение .

Решение будет зависеть от неизвестного р. От этой зависимости можно избавиться, если потребовать, чтобы

.

Тогда используя неравенство , получим

 ,

и для определения n имеем уравнение

 .

По таблице можно найти для которых .  Тогда и .

В практических расчетах обычно используют значения 2, равные 0,05 и 0,01. Для этих значений соответствующие равны 1,96 и 2,576.  

Пример 5 

Вероятность того, что деталь не стандартна, равна р = 0,1. Найти сколько деталей нужно отобрать, чтобы с вероятностью 0,9544 можно было утверждать, что относительная частота появления нестандартных деталей (среди отобранных) отклонится от постоянной вероятности р по абсолютной величине не больше, чем на 0,03.

Решение. 

Согласно условиям задачи p = 0,1, q = 0,9, . По формуле

находим

.

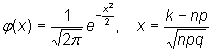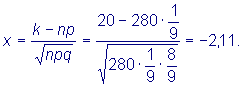
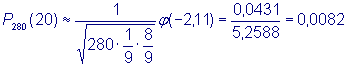
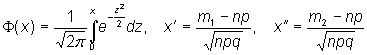Следовательно . По таблице находим . Отсюда искомое число деталей n = 400.