ODE Lecture 6.1.

Темы | Предыдущий пункт | Следующий пункт | Литература

Лекция 2.3.

Плоскость и виды ее уравнения в пространстве.

2.3.5. Угол между двумя плоскостями. Точка пересечения трех плоскостей.

Пусть заданы уравнения двух плоскостей в общем виде:

(1)

Углом между этими плоскостями называется любой из двух смежных двугранных углов, образованных этими плоскостями ( в случае параллельности плоскостей угол между ними можно считать равными 0 или ). Один из этих двугранных углов равен углу , образованному нормальными векторами плоскостей: и .

Угол между двумя векторами и находится по формуле:

(2)

Условие перпендикулярности двух плоскостей: если плоскости, заданные уравнениями (1) перпендикулярны, то

, тогда из формулы (2) следует:

это и есть условие перпендикулярности двух плоскостей.

Пример 1. Доказать, что плоскости x + y + z = 0; и x + y - 2z + 3 = 0 перпендикулярны.

Решение. Проверим условие перпендикулярности плоскостей, то есть:

,

,

, следовательно плоскости перпендикулярны.

Условие параллельности двух плоскостей: если плоскости, заданные уравнениями (1) параллельны, то их нормальные векторы коллинеарны, то есть:

и тогда из условия коллинеарности векторов следует:

это и есть условие параллельности плоскостей.

Пример 2. Доказать, что плоскости x + y - z = 0; 2x + 2y - 2z + 3 = 0 параллельны.

Решение. Проверим выполнение условия параллельности плоскостей, то есть:

, следовательно плоскости параллельны.

Чтобы найти точку пересечения трех плоскостей, заданных уравнениями:

Нужно решить эти уравнения совместно:

Пример 3. Найти точку пересечения плоскостей: x - y + z = 0; x + 2y - 1 = 0; x + y - z + 2 = 0.

Решение. Решим систему уравнений:

.

Воспользуемся методом Крамера:

.

,

,

.

А(- 1, 1, 2) - точка пересечения.
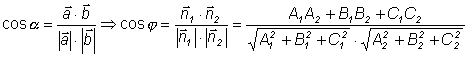
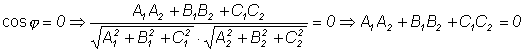
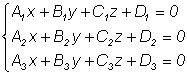
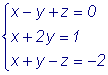
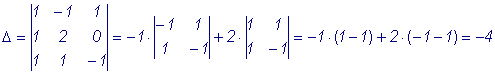
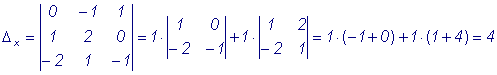
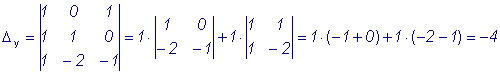
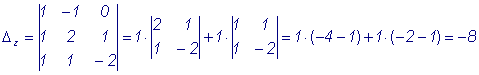