| Темы | Предыдущий пункт | Следующий пункт | Литература |
|
|
 Плоскость
и виды ее уравнения в пространстве.
Плоскость
и виды ее уравнения в пространстве.
|
|
2.3.6. Расстояние от точки до плоскости. Отклонением данной точки от данной плоскости называется число d, равное длине перпендикуляра, опущенного из этой точки на плоскость, взятой со знаком плюс, если точка и начало координат лежат по разные стороны от данной плоскости, и со знаком минус, если они лежат по одну сторону от плоскости. Очевидно, что расстояние от точки до плоскости равно абсолютной величине отклонения.
Пусть требуется найти расстояние от
точки
Задача состоит в том, чтобы
найти длину перпендикуляра
Заметим, что
Числовой множитель d, взятый по абсолютной
величине, очевидно,
дает нам искомое расстояние. Знак d будет положительным, если
векторы При одинаковом
направлении векторов Из рисунка видно, что или Но точка К лежит на
плоскости, поэтому ее радиус-вектор или Рассматривая полученное
выражение, замечаем, что оно есть
результат подстановки Выражая скалярное
произведение через координаты
векторов Таким образом, чтобы найти отклонение точки от плоскости, надо в левую часть нормального уравнения плоскости, записанного в координатной форме, вместо текущих координат подставить координаты данной точки, а для вычисления расстояния от точки до плоскости следует взять абсолютную величину отклонения.
Пример. Найти расстояние от точки A(1, 2, 3) до плоскости 2x - 2y + z - 3 = 0. Решение. По условию имеем общее уравнение плоскости. Приведем его к нормальному виду:
Найдем отклонение d:
расстояние от точки А до плоскости равно:
|
|
|
|
|
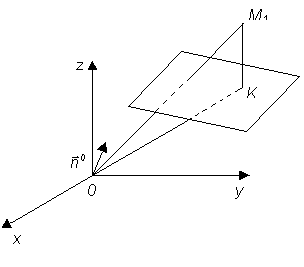 Рис.
1.
Рис.
1.