| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Производная и дифференциал |
|
|
|
|
|
3.2.2. Механический и геометрический смысл производной
|
|
|
Механический смысл производной Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v – скорость равномерного движения. Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние s будет зависеть от времени t, т.е. будет функцией времени. Итак, пусть материальная точка движется по прямой в одном направлении по закону s = s(t). Отметим некоторый момент времени t0. К этому моменту точка прошла путь s=s(t0). Определим скорость v материальной точки в момент времени t0. Для этого рассмотрим какой-нибудь другой момент времени
t0+ Рассмотрим отношение Итак, скоростью движения в данный момент времени
t0
(мгновенной скоростью) называется предел средней скорости в промежутке от
t0 до t0+
т.е. скорость неравномерного движения это производная от пройденного пути по времени. Геометрический смысл производной
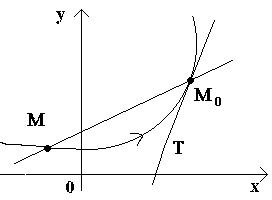
Введем сначала определение касательной к кривой в данной точке. Пусть имеем кривую и на ней фиксированную точку М0 (см. рисунок).
Рассмотрим другую точку М этой кривой и проведем секущую M0M. Если точка М начинает перемещаться по кривой, а точка М0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М0 с любой стороны секущая стремится занять положение определенной прямой М0Т, то прямая М0Т называется касательной к кривой в данной точке М0. Т.о., касательной к кривой в данной точке М0 называется предельное положение секущей М0М, когда точка М стремится вдоль кривой к точке М0. Рассмотрим теперь непрерывную функцию y
= f(x) и
соответствующую этой функции кривую. При некотором значении
х0 функция принимает значение
y0= f(x0). Этим значениям x0
и y0 на кривой соответствует точка
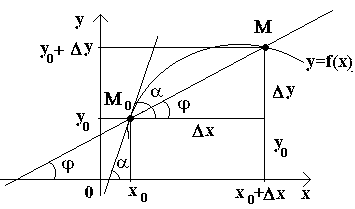
М0 (x0; y0). Дадим аргументу
x0 приращение Если теперь
т.е. f '(x) = tg
Т.о., геометрически у '(x0) представляет угловой коэффициент касательной к графику этой функции в точке x0, т.е. при данном значении аргумента x, производная равна тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке М0 (x; y) с положительным направлением оси Ox. |
|
|
|
|
|