| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|
 Производная
и дифференциал
Производная
и дифференциал
|
|
|
|
|
|
3.2.3. Дифференцируемость функций. Непрерывность дифференцируемой функции
|
|
|
Функция y=f(x) называется дифференцируемой
в некоторой
точке x0, если она имеет в этой точке определенную
производную, т.е. если предел отношения Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b). Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y = f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна. Таким образом, из дифференцируемости функции следует ее непрерывность. Доказательство: Если где
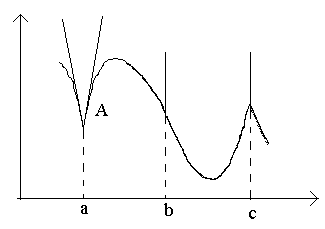
а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать. Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной). Рассмотрим на рисунке точки а, b, c.
В точке a при В точке b при Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" c вертикальной касательной. В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.
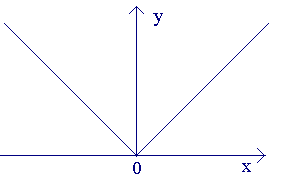
Пример Рассмотрим функцию y=|x|.
Эта функция непрерывна в точке x = 0, т.к.
Покажем, что она не имеет производной в этой точке.
Но тогда при
А при
Т.о., отношение
|
|
|
|
|
|