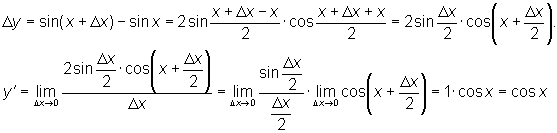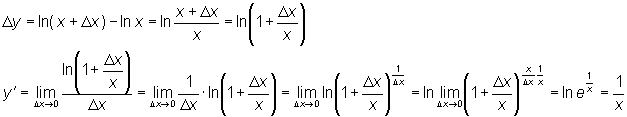| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Производная и дифференциал |
|
|
|
|
3.2.4. Производные некоторых основных элементарных функций |
|
1. y = xn
Если n - целое положительное число, то, используя формулу бинома Ньютона:
Можно доказать, что
Итак, если x получает
приращение
Заметим, что в каждом из
пропущенных слагаемых есть множитель Найдем предел:
Мы доказали эту формулу для 2. y = sin x. Вновь воспользуемся определением производной. Так как
Таким образом, Аналогично можно показать, что
3. y = ln x Имеем
Итак,
Используя свойства логарифма можно показать, что
|
|
|
|
|