| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Первообразная функции. Неопределенный интеграл. |
|
|
|
|
|
4.1.1. Основные свойства неопределенного интеграла |
|
1. Дифференциал неопределенного интеграла 2. Неопределенный интеграл от дифференциала непрерывно
дифференцируемой функции равен самой этой функции с точностью до
постоянной: 3. Постоянный множитель можно выносить за знак неопределенного
интеграла: 4. Неопределенный интеграл от суммы двух непрерывных функций
равен сумме неопределенных интегралов от этих функций: 5. Если F(x) есть первообразная функции f(x) ,
то Данные свойства вытекают непосредственно из определения неопределенного интеграла. (см пункт 4.1) |
|
|
|
|
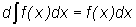 равен подынтегральному выражению, т. е.
равен подынтегральному выражению, т. е. 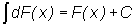
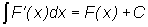 .
.
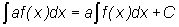 где
где 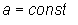 .
.
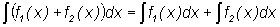 .
.
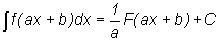 .
.