;    ;    .

Примерами противоположных событий могут служить попадание и промах при выстреле, отказ прибора в данном интервале времени и его исправная работа в том же интервале времени.

Для каждой пары событий А и В введем операции объединения и пересечения.

Событие заключающееся в том, что из двух событий А и В происходит по крайней мере одно, называют объединением событий А и В.

Событие (АВ), заключающееся в том, что происходят одновременно оба события А и В, называют пересечением событий А и В.

Операции объединения и пересечения коммутативны и ассоциативны

;
;
;
.

Следующие формулы вводятся как аксиомы:

Введенные соотношения переносятся с двух событий на произвольное конечное непустое семейство событий .

Операции объединения и пересечения, наконец, дистрибутивны по отношению друг к другу:

;
.

Структура, которая образуется на множестве событий введенными определениями и аксиомами, называется структурой булевой алгебры. Рассмотрим вспомогательные понятия, определяемые на булевой алгебре событий.

Два события А и В, для которых называются непересекающимися (взаимно исключающими). Объединение таких событий называют суммой и обозначают А + В вместо .

Разностью двух событий А и В называют событие А – В, состоящие в том, что произойдет событие А и не произойдет событие В. Очевидно, что .

Симметрической разностью двух событий А и В называют событие , означающее, что происходит лишь одно из А, В.

События образуют полную группу событий, если они попарно не пересекаются (несовместны) и , то есть в результате эксперимента происходит одно и только одно из них.

Говорят, что событие А влечет событие В (обозначают ), если событие В обязательно происходит при появлении события А. Если события А и В могут появиться или не появиться только вместе, то есть и , то они называются эквивалентными (А = В). Эквивалентные события различать не будем. Отношение «влечет» является отношением порядка в множестве событий.

.

Для строгого математического обоснования, вводят понятие элементарного события.

Элементарным событием называется событие, не содержащее никаких подсобытий, кроме невозможного события и самого себя

В рамках эксперимента, элементарное событие это результат эксперимента. Каждое, относящееся к рассматриваемой модели элементарное событие, влечет либо наступление, либо не наступление каждого данного события, связанного с рассматриваемой моделью. Например, при одном выстреле по мишени элементарным событием будут промах и попадание. В эксперименте – при двух выстрелах по мишени будет одно попадание – элементарными событиями будут: попадание при первом и промах при втором выстреле и промах при первом и попадание при втором выстреле.

Случайный эксперимент называется конечным, если имеется полная группа элементарных событий.

Достоверное событие представляет собой множество всех элементарных событий . Невозможное событие представляет собой пустое множество .

Например, пространство элементарных событий в эксперименте, заключающемся в том, что наблюдается попадание или промах при двух выстрелах по мишени состоит из четырех элементарных событий: два попадания, попадание – промах, промах – попадание, два промаха.

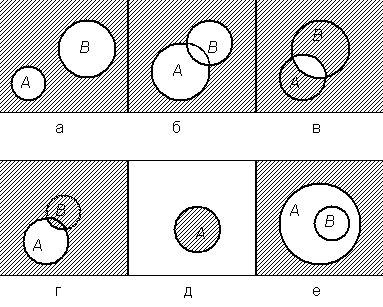
На рисунках представлены изображения следующих операций:

Важным примером случайного эксперимента является эксперимент, в котором измеряется некоторая величина Х. В качестве элементарных событий здесь можно взять события вида         (Х = х), где х – некоторое фиксированное значение. Множество элементарных событий естественно отождествить с множеством точек на прямой. Если априори известно, что Х может принимать лишь значения из некоторого множества М, то это множество и следует рассматривать как множество элементарных событий. В процессе измерения естественно предполагать возможность наблюдения события , где а  и  b – произвольные числа. Всевозможные конечные суммы таких полуинтервалов можно рассматривать как алгебру событий, связанных с экспериментом.