где q = 1 - p. Постоянные n и p, входящие в это выражение, являются параметрами биномиального закона распределения. Этим законом описывается распределение вероятностей только дискретной случайной величины. Возможными значениями случайной величины Х являются m = 0, 1, ... , n. 

Биномиальному распределению подчиняются, например, число бракованных изделий в выборках из неограниченной партии продукции. Биномиальное распределение может быть задано в виде таблицы

Х = m	0	1	2	...	k	...	n

и в виде функции распределения

.

Найдем числовые показатели случайной величины, подчиняющейся биномиальному распределению. Для этого запишем выражения начальных моментов до 2 порядка включительно:

,

(1)

,

(2)

Для вычисления сумм в этих формулах продифференцируем несколько раз по р выражение

.

В результате получим

,

(3)

Умножая обе части равенства (3) на р, получим

,

(4)

В силу равенства первых частей соотношений (1) и (4), заключаем

.

Учитывая, что p + q = 1, имеем , или M(x) = np.

Таким образом, математическое ожидание числа появлений события в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.

Используя связь между центральными и начальными моментами, получим выражение для дисперсии и среднеквадратичного отклонения для биномиального распределения

,

(5)

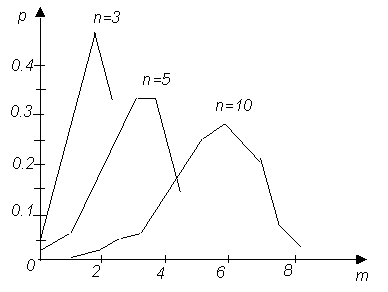
Исследуем форму графиков биномиальных распределений. Сначала при фиксированном n и меняющимся р, затем при фиксированном р и возрастающем n

,

Рис. 1

,

Рис. 2

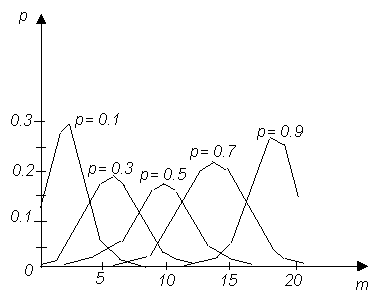
На рисунке 1 построены многоугольники биномиального распределения при n = 20 и p = 0,1; 0,3; 0,5; 0,7 и 0,9. Особенностью этих распределений является то, что вероятность Pn(m) сначала возрастает при увеличении m и достигает наибольшего значения при некотором наивероятнейшем значении m = m. которое можно определить из двойного неравенства

Значение m является модой биномиального закона. Если имеются два наивероятнейших значения, то распределения является бимодальным.

Если np - целое число, то математическое ожидание и мода совпадают. После достижения наивероятнейшего значения m₀ вероятность P_n(m) начинает убывать.

В заключение отметим, что биномиальное распределение широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и. т. д.
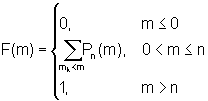