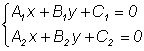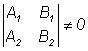(1)

Каждое из уравнений (1) в отдельности определяет прямую. Каждое их совместное решение определяет общую точку этих прямых. Пусть определитель этой системы не равен нулю:

Значит система совместна и имеет единственное решение. Прямые пересекаются в одной точке, эти прямые различны и не параллельны друг другу.

Предположим теперь, что , то есть или .Здесь в свою очередь имеются две возможности:

или .

Рассмотрим первую из них. Обозначим каждое из равных отношений буквой q, тогда имеем:

Умножим второе из уравнений (1) на q и вычтем полученное соотношение из первого уравнения; получим:. Это соотношение противоречиво, так как . Значит система (1) не имеет совместных решений. В данном случае уравнения (1) определяют прямые , не имеющие ни одной общей точки, то есть параллельные.

Рассмотрим вторую из двух указанных выше возможностей:

.

Коэффициенты уравнений пропорциональны. Уравнения (1) определяют одну и туже прямую.

Задачи для самостоятельного решения.