| Темы | Предыдущий пункт | Следующий пункт | Литература | ||||||||||||||
|
|
||||||||||||||
 Уравнение
прямой на плоскости.
Уравнение
прямой на плоскости.
|
||||||||||||||
|
2.1.6 Нормальное уравнение прямой. Задача вычисления расстояния от точки до прямой. Рассмотрим один специальный вид записи уравнения прямой, известной под названием нормального уравнения прямой. Пусть дана какая-нибудь прямая. Проведем через начало координат прямую n, перпендикулярную данной, - мы будем называть ее нормалью, - и обозначим буквой Р точку, в которой она пересекает данную прямую (рис. 1).
На нормали введем
положительное направление от точки О
к точке Р. Обозначим через
Найдем выражение проекции
отрезка ОМ на нормаль через координаты
точки М. Обозначим через
Таким образом:
Из равенств (1) и (2) следует, что:
Уравнение прямой,
написанное в форме (3) называется
нормальным. В этом уравнении Условимся называть отклонением точки
М* от данной прямой число +d, если М* лежит
по ту сторону от прямой, куда идет
положительное направление нормали, и -d,
если М* лежит с другой стороны от данной
прямой. Отклонение точки от прямой
будем обозначать буквой
Полезно заметить, что,
когда точка М* и начало координат лежат
по разные стороны от прямой
Одной из стандартных задач аналитической геометрии является задача вычисления отклонения точки от прямой. Эта задача решается следующей теоремой: Теорема. Если точка М* имеет координаты (х*, у*), а прямая задана нормальным уравнением
то отклонение точки М* от этой прямой задается формулой:
Покажем, как привести общее уравнение прямой к нормальному виду. Пусть
- общее уравнение прямой, а
- ее нормальное уравнение. Так как уравнения (5) и (6)
определяют одну и ту же прямую, то
коэффициенты этих уравнений
пропорциональны. Умножим все члены
уравнения (5) на некоторый множитель
Для одной и той же прямой будем иметь:
Чтобы найти множитель
Отсюда:
Число
Пример. Даны прямая 3х - 4у + 10 = 0 и точка М(4;3). Найти отклонение точки М от данной прямой. Решение. Подставляя координаты точки М, имеем:
Итак, точка М имеет отрицательное
отклонение от данной прямой и удалена
от нее на расстояние d = 2. |
|
|
|
|
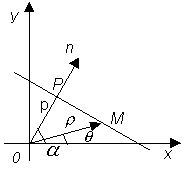 Рис.
1.
Рис.
1.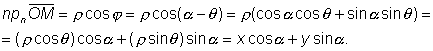
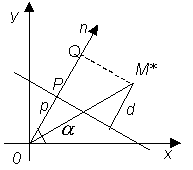 Рис.
2
Рис.
2