| Темы | Предыдущий пункт | Следующая лекция | Литература |
|
|
 Плоскость
и виды ее уравнения в пространстве.
Плоскость
и виды ее уравнения в пространстве.
|
|
2.3.7. Основные задачи на составление уравнения плоскости. Задача 1. Составить уравнение плоскости,
проходящей через данную точку Решение. Пусть M(x, y, z) - произвольная точка плоскости. По условию вектор
Это и есть уравнение плоскости, проходящей через данную точку, перпендикулярно вектору.
Задача 2. Составить уравнение плоскости,
проходящей через данную точку,
параллельно двум неколлинеарным
векторам Решение. Пусть точка M(x, y,
z) –
произвольная точка плоскости, тогда
векторы
или в координатной форме:
Это и есть уравнение плоскости, проходящей через данную точку, параллельно двум другим векторам.
Задача 3.
Составить уравнение плоскости,
проходящей через три данные точки: Решение. Возьмем
произвольную точку плоскости M(x, y,
z) и
соединим одну из данных точек, например
или в координатной форме:
Это и есть уравнение плоскости, проходящей через три заданные точки.
|
|
|
|
|
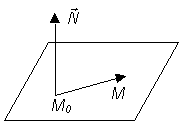 Рис.
1.
Рис.
1.
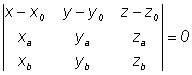 .
.
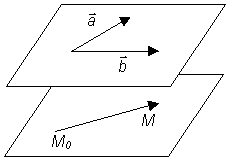 Рис.2.
Рис.2.
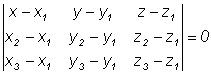 .
.