| Темы | Предыдущий пункт | Следующий пункт | Литература | ||
|
|
||
Лекция 2.4. 
Прямая
линия в пространстве.
|
||
|
2.4.2. Угол между прямыми. Условие принадлежности двух прямых одной плоскости. Углом между двумя прямыми в пространстве будем называть любой из углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. При этом условимся брать угол от 0 до 180 градусов, если не сделано дополнительных условий. Пусть заданы две прямые:
За угол между ними можно
принять угол между направляющими
векторами
В этой формуле можно ставить любой знак, что соответствует выбору одного из двух различных углов между прямыми. В случае перпендикулярности
двух прямых, угол между ними Это и есть условие
перпендикулярности двух прямых. Две прямые в пространстве могут
пересекаться, быть параллельными и
скрещиваться. Если две прямые
пересекаются или параллельны, то они
лежат в одной плоскости. Пусть две
прямые заданы каноническими
уравнениями:
где
|
и 
.
и 
.
Поэтому:
и 
и из формулы (1) получаем:
.
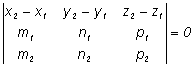- условие параллельности двух
прямых.
и 
- точки принадлежащие прямым.
Очевидно, чтобы прямые лежали в одной
плоскости необходимо и достаточно
чтобы векторы 
были компланарны, то есть их смешанное
произведение равно нулю:
- условие принадлежности двух прямых
одной плоскости.
|
|
|
|