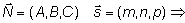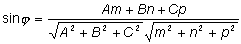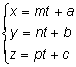| Темы | Предыдущий пункт | Литература | ||||||||||||
|
|
||||||||||||
 Прямая
линия в пространстве.
Прямая
линия в пространстве.
|
||||||||||||
|
2.4.3. Прямая и плоскость.
1. Угол
между прямой и плоскостью.
Пусть заданы прямая Углом Найдем синус угла
где 2. Условие параллельности и
перпендикулярности прямой и плоскости.
Если прямая Это и есть условие параллельности прямой и плоскости. Условие перпендикулярности прямой и плоскости совпадает с
условием параллельности этой прямой и перпендикуляра к плоскости, то есть: 3. Пересечение прямой с
плоскостью Пусть заданы уравнения
прямой и плоскость: Координаты точки
пересечения прямой и плоскости должны
одновременно удовлетворять уравнениям
(4) и (5), а поэтому для определения
координат точки пересечения нужно
совместно решить эти два уравнения. Запишем уравнение (4) в
параметрическом виде: Равенства (6) подставим в уравнение (5): A(mt
+ a) + B(nt + b) + C(pt + c) = 0.
Отсюда получим t:
Подставляя найденное
значение t
в формулы (6), найдем x,
y,z, то есть координаты точки
пересечения прямой и плоскости.
Решение. Уравнение плоскости, проходящей через данную прямую имеет вид:
(Уравнение пучка плоскостей) Условие прохождения этой плоскости через точку М(1, 1, -1) дает:
или 5x - y + z - 3 = 0 - это и есть искомое уравнение плоскости. |
|
|
|
|
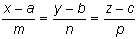 и плоскость Ax + By + Cz + D = 0 .
и плоскость Ax + By + Cz + D = 0 .
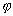 между
прямой и плоскостью называется любой
из двух смежных углов, образованных
прямой и ее проекцией на плоскость.
между
прямой и плоскостью называется любой
из двух смежных углов, образованных
прямой и ее проекцией на плоскость.
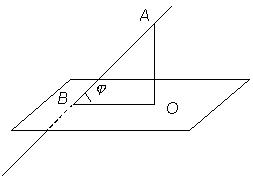 Рис. 1.
Рис. 1.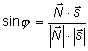 ,
,