Уравнение
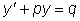 , где
, где
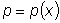 и
и
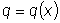 - заданные непрерывные функции, называется линейным
дифференциальным уравнением первого порядка.
- заданные непрерывные функции, называется линейным
дифференциальным уравнением первого порядка.
Если функция
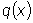 , стоящая в правой части
уравнения, тождественно равна нулю, т.е.
, стоящая в правой части
уравнения, тождественно равна нулю, т.е.
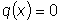 ,
,
то уравнение называется линейным однородным,
в противном случае - линейным неоднородным.
Таким образом,
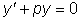 - линейное однородное уравнение,
а
- линейное однородное уравнение,
а 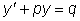 - линейное неоднородное уравнение.
- линейное неоднородное уравнение.
Рассмотрим два метода интегрирования линейных уравнений.
I метод - метод Бернулли
Для решения уравнения применим подстановку y=UV,
причем функцию U=U(x) будем считать новой
неизвестной функцией, а функцию
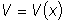 мы выберем произвольно,
подчинив некоторому условию.
Так как при этом
мы выберем произвольно,
подчинив некоторому условию.
Так как при этом 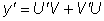 ,
то эта подстановка дает:
,
то эта подстановка дает:
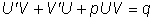
и
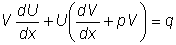 .
.
Используя произвольный
выбор функции V,
подчиним ее условию:
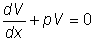 .
.
Разделяя переменные и
интегрируя в последнем равенстве, получаем:
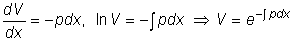 .
.
Поэтому исходное уравнение
после подстановки полученной функции V(x) имеет вид:
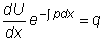 .
.
Это уравнение также является
уравнением с разделяющимися переменными.
Решая его, получаем:
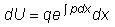 ,
,
а после интегрирования
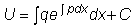 .
.
Возвращаясь к переменной
y=UV имеем общее решение
линейного неоднородного уравнения:
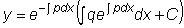 .
.

Пример
Решить уравнение
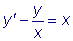 .
.
Здесь
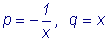 .
.
Имеем:
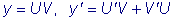
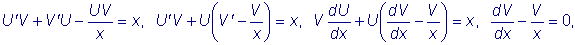
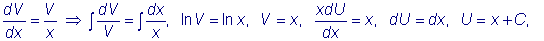
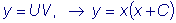 - общее решение линейного уравнения.
- общее решение линейного уравнения.
II метод - метод вариации произвольной постоянной - метод
Лагранжа
В линейном однородном уравнении
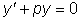 переменные разделяются и его общее решение,
которое мы обозначим через Y , легко находится:
переменные разделяются и его общее решение,
которое мы обозначим через Y , легко находится:
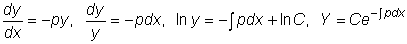 .
.
Будем теперь находить общее решение неоднородного линейного уравнения
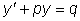 ,
считая, что общее решение неоднородного уравнения y имеет такую
же форму, как и общее решение соответствующего однородного уравнения
Y , но где C есть не постоянная величина, а неизвестная
функция от x , т.е. считая, что
,
считая, что общее решение неоднородного уравнения y имеет такую
же форму, как и общее решение соответствующего однородного уравнения
Y , но где C есть не постоянная величина, а неизвестная
функция от x , т.е. считая, что
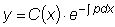 .
.
Дифференцируя это выражение
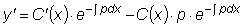
и подставляя в
рассматриваемое неоднородное уравнение, получим:
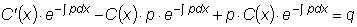 или
или
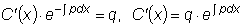 .
.
Откуда находим функцию
C(x) :
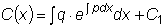 .
.
Таким образом,
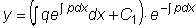
или
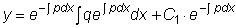 .
.
Полученное общее решение состоит из двух слагаемых, из которых второе
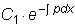 является общим решением
соответствующего однородного уравнения, а первое
является общим решением
соответствующего однородного уравнения, а первое
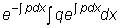 является частным решением неоднородного уравнения, получаемым из
общего при
является частным решением неоднородного уравнения, получаемым из
общего при  .
.

Пример
Найти общее решение уравнения
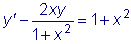 .
.
Интегрируем соответствующее однородное уравнение:
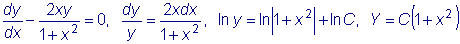 .
.
Считаем C функцией x :
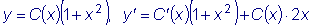
Подставляем в исходное уравнение:
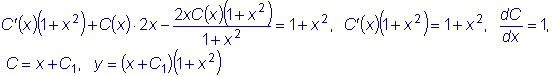 .
.
 Задачи для самостоятельного решения
Задачи для самостоятельного решения

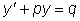 , где
, где
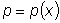 и
и
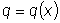 - заданные непрерывные функции, называется линейным
дифференциальным уравнением первого порядка.
- заданные непрерывные функции, называется линейным
дифференциальным уравнением первого порядка. 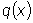 , стоящая в правой части
уравнения, тождественно равна нулю, т.е.
, стоящая в правой части
уравнения, тождественно равна нулю, т.е.
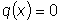 ,
,
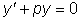 - линейное однородное уравнение,
а
- линейное однородное уравнение,
а 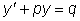 - линейное неоднородное уравнение.
- линейное неоднородное уравнение.
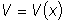 мы выберем произвольно,
подчинив некоторому условию.
Так как при этом
мы выберем произвольно,
подчинив некоторому условию.
Так как при этом 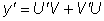 ,
то эта подстановка дает:
,
то эта подстановка дает:
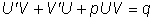
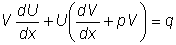 .
.
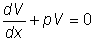 .
.
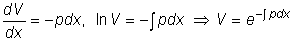 .
.
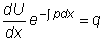 .
.
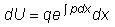 ,
,
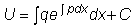 .
.
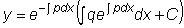 .
.
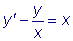 .
.
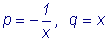 .
.
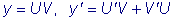
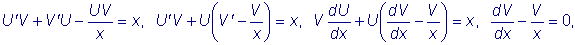
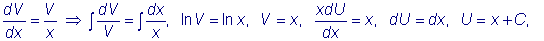
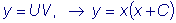 - общее решение линейного уравнения.
- общее решение линейного уравнения. 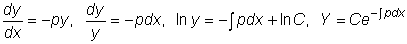 .
. 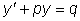 ,
считая, что общее решение неоднородного уравнения y имеет такую
же форму, как и общее решение соответствующего однородного уравнения
Y , но где C есть не постоянная величина, а неизвестная
функция от x , т.е. считая, что
,
считая, что общее решение неоднородного уравнения y имеет такую
же форму, как и общее решение соответствующего однородного уравнения
Y , но где C есть не постоянная величина, а неизвестная
функция от x , т.е. считая, что
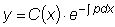 .
.
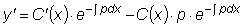
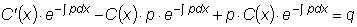 или
или
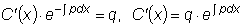 .
.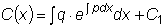 .
.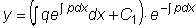
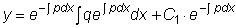 .
. 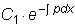 является общим решением
соответствующего однородного уравнения, а первое
является общим решением
соответствующего однородного уравнения, а первое
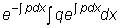 является частным решением неоднородного уравнения, получаемым из
общего при
является частным решением неоднородного уравнения, получаемым из
общего при  .
.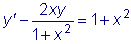 .
.
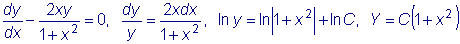 .
. 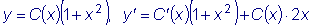
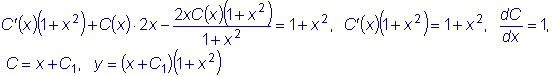 .
.