| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Дифференциальные уравнения первого порядка |
|
|
|
|
|
6.1.4. Уравнение Бернулли |
|
Уравнением Бернулли называется уравнение вида dy/dx + P(x)y = Q(x)y n. При n = 0 или n = 1 уравнение становится линейным, методы интегрирования которого рассматривались в предыдущем пункте. Есть следующие два способа интегрирования этого уравнения. 1. Уравнение приводится к линейному. Разделив все члены такого уравнения на y n, получим: y -n(dy/dx) + P(x)y -n+1 = Q(x). Сделаем замену: y -n+1 = z. Тогда dz/dx = (-n+1)y -ndy/dx. После подстановки этих выражений в уравнение оно примет вид: dz/dx + (1-n)P(x)z = (1-n)Q(x). Это линейное уравнение относительно функции z. После его интегрирования возвращаемся к переменной y, подставив вместо z выражение y 1-n. Получим общий интеграл уравнения Бернулли. 2. Уравнение решается по методу Бернулли с подстановкой y = UV, уже использованному для решения линейных неоднородных уравнений. Пример
Найти общее решение уравнения
x(dz/dx) - z = -ln(x).
Это линейное уравнение относительно функции z . Применим метод вариации
произвольной постоянной:
следовательно Заменяя теперь z
на |
|
|
|
|
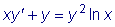 .
.
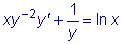 .
.
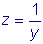 ,
тогда
,
тогда 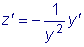 .
.
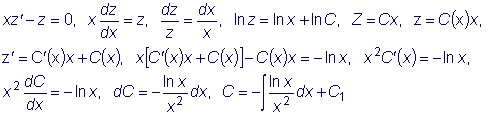
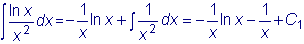 ,
,
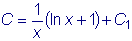 ,
,
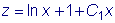 .
.
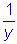 ,
,
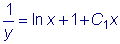 или
или
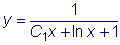 .
.