Методы решения линейных однородных уравнений второго порядка
переносятся и на линейные однородные уравнения любого порядка.
Не останавливаясь на доказательствах, рассмотрим метод решения
линейного однородного уравнения n -го порядка с постоянными
коэффициентами
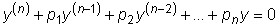 .
.
Общее решение этого уравнения находится следующим образом:
1. Составляем характеристическое уравнение
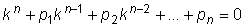 .
.
2. Находим корни характеристического уравнения
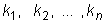 .
.
3. По характеру корней выписываем частные линейно независимые решения,
руководствуясь тем, что:
а) каждому действительному однократному корню k соответствует
частное решение e kx ;
б) каждому действительному корню k кратности r
соответствуют r линейно независимых частных решений
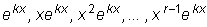 ;
;
в) каждой паре комплексных сопряженных корней
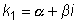 и
и
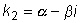 соответствуют два частных решения
соответствуют два частных решения
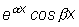 и
и
 ;
;
г) каждой паре комплексных сопряженных корней
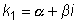 и
и
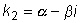 кратности t
соответствуют 2t частных решений:
кратности t
соответствуют 2t частных решений:
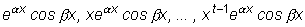 и
и
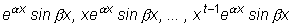 .
.
Этих частных решений будет столько, какова степень характеристического
уравнения, т.е. столько, каков порядок данного уравнения.
4.Зная n линейно независимых частных решений
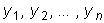 , записываем общее решение
заданного уравнения:
, записываем общее решение
заданного уравнения:
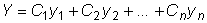 , где
, где
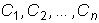 - произвольные постоянные.
- произвольные постоянные.

Пример
Найти общее решение уравнения
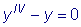 .
.
Характеристическое уравнение
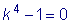
имеет корни
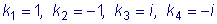 . Общее решение запишется:
. Общее решение запишется:
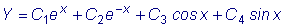 .
.
Замечание
Функции 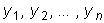 называются линейно зависимыми в некотором интервале, если
существуют такие одновременно не равные нулю постоянные
называются линейно зависимыми в некотором интервале, если
существуют такие одновременно не равные нулю постоянные
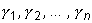 , что
, что
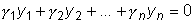 во всех точках
рассматриваемого интервала. Если таких постоянных не существует, то
функции называются линейно независимыми .
Для двух функций это определение эквивалентно принятому ранее.
во всех точках
рассматриваемого интервала. Если таких постоянных не существует, то
функции называются линейно независимыми .
Для двух функций это определение эквивалентно принятому ранее.

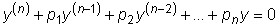 .
. 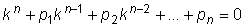 .
. 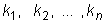 .
. 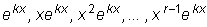 ;
; 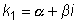 и
и
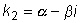 соответствуют два частных решения
соответствуют два частных решения 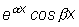 и
и
 ;
; 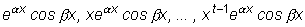 и
и
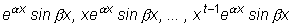 .
. 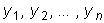 , записываем общее решение
заданного уравнения:
, записываем общее решение
заданного уравнения:
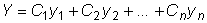 , где
, где
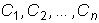 - произвольные постоянные.
- произвольные постоянные.
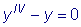 .
. 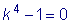
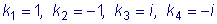 . Общее решение запишется:
. Общее решение запишется: 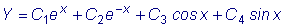 .
. 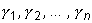 , что
, что
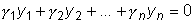 во всех точках
рассматриваемого интервала. Если таких постоянных не существует, то
функции называются линейно независимыми .
Для двух функций это определение эквивалентно принятому ранее.
во всех точках
рассматриваемого интервала. Если таких постоянных не существует, то
функции называются линейно независимыми .
Для двух функций это определение эквивалентно принятому ранее.