Рассмотрим линейное неоднородное уравнение n -го порядка
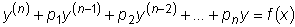
с постоянными коэффициентами
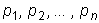 . .
В этом случае, как и в случае уравнения второго порядка, общее решение
представляется как сумма какого-нибудь частного решения линейного
неоднородного уравнения и общего решения соответствующего однородного
уравнения, т.е. y = Y + y* .
Частное решение y*
можно всегда найти, используя метод вариации произвольных постоянных.
Но мы ограничимся указанием только тех случаев, когда частное решение
y* можно найти, не прибегая к интегрированию.
1. Пусть
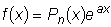 , ,
тогда надо различать два случая:
а) a не является корнем характеристического уравнения.
В этом случае частное решение нужно искать в виде
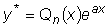 . .
б) a является корнем кратности t характеристического
уравнения.
Частное решение y*
в этом случае нужно искать в форме
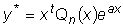 . .
2. Пусть 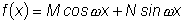 ,
где M и N - постоянные коэффициенты. ,
где M и N - постоянные коэффициенты.
Тогда вид частного решения определяется следующим образом:
а) 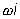 не является корнем
характеристического уравнения, не является корнем
характеристического уравнения,
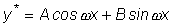 . .
б) 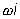 корень характеристического уравнения кратности t ,
корень характеристического уравнения кратности t ,
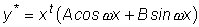 . .
3. Пусть 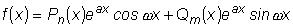 , тогда: , тогда:
а) 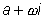 не является корнем характеристического уравнения,
не является корнем характеристического уравнения,
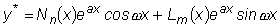 . .
б) 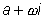 является корнем
характеристического уравнения кратности t , является корнем
характеристического уравнения кратности t ,
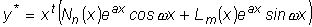 . .

Пример 1.
Найти общее решение уравнения
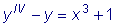 . .
Характеристическое уравнение
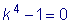
имеет корни
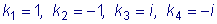 . .
Общее решение линейного однородного уравнения запишется:
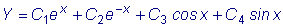 . .
Частное решение неоднородного уравнения ищем в форме
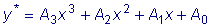 . .
Дифференцируя
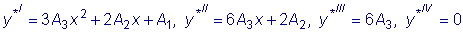
и подставляя в
исходное уравнение, получим:
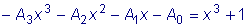 . .
Приравнивая коэффициенты при одинаковых степенях x , находим:
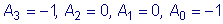 . .
Следовательно,
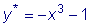 , ,
а общее решение
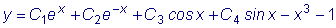 . .

Пример
2.
Решить уравнение
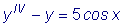 . .
Как и в предыдущем примере, здесь
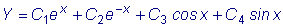 . .
Частное решение
y * ищем в форме
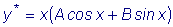 , ,
т.к. i
является корнем характеристического уравнения. Дифференцируя
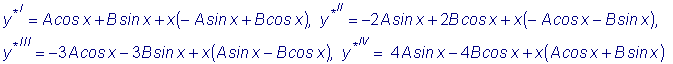
и подставляя в исходное уравнение, получим:
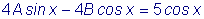 , ,
откуда
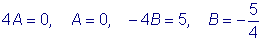 . .
Следовательно,
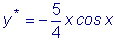
и общее решение
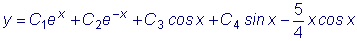 . .
 Задачи для самостоятельного решения.
Задачи для самостоятельного решения.
|

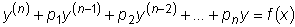
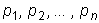 .
. 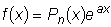 ,
, 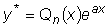 .
. 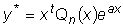 .
. 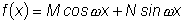 ,
где M и N - постоянные коэффициенты.
,
где M и N - постоянные коэффициенты. 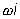 не является корнем
характеристического уравнения,
не является корнем
характеристического уравнения, 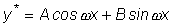 .
. 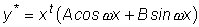 .
. 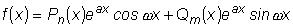 , тогда:
, тогда: 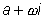 не является корнем характеристического уравнения,
не является корнем характеристического уравнения,
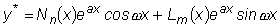 .
. 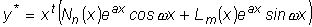 .
.
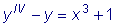 .
.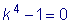
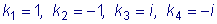 .
. 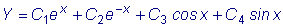 .
. 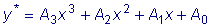 .
. 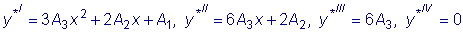
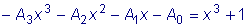 .
. 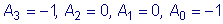 .
.
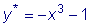 ,
,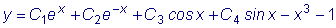 .
. 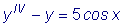 .
.
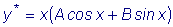 ,
, 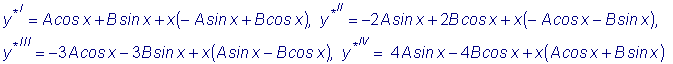
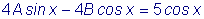 ,
, 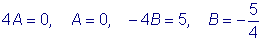 .
. 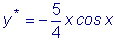
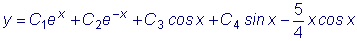 .
.